一、选择题(16分)
1.计算鱼缸能装水多少升,是求鱼缸的( )。
A.表面积 B.棱长总和 C.体积 D.容积
2.营养学家建议:儿童每天水的摄入量应不少于1500mL。要达到这个要求,小明每天用底面直径6cm,高10cm的圆柱形水杯喝水,至少喝水( )杯。
A.4 B.5 C.6 D.7
3.两个圆柱形容器内原来的水面高度都是6cm。它们的底面直径都是10cm。①号容器内放入一个小球后,水面高度为10cm。②号容器内放入一个小球和一个大球,水面高度为16cm。两个容器内的小球完全相同,水也均未溢出,小球的体积与大球的体积的比是( )。
A.5∶8 B.2∶5 C.2∶3 D.5∶12
4.制作一个无盖的圆柱形容器,应该选择( )。
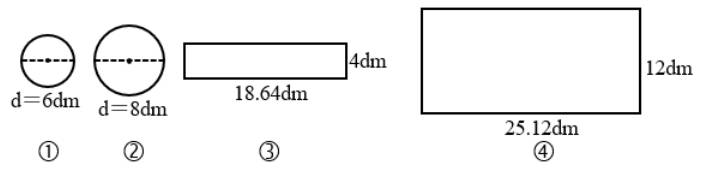
A.①和③ B.①和④ C.②和③ D.②和④
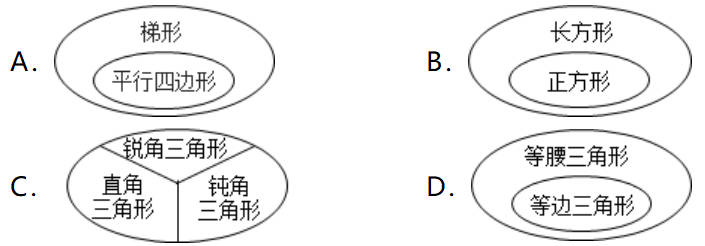
5.下面各图中,( )是不正确的。
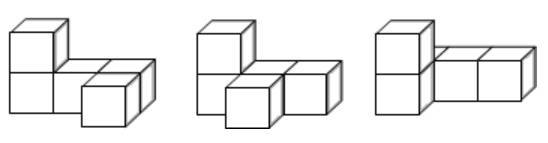
6.如图是由7个立方体摆成的几何体,从右面观察到的图形是( )。
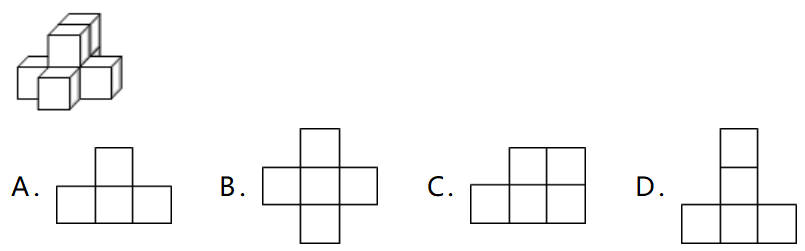
7.一个三角形,三个内角度数比是2∶3∶1,这个三角形按角分是( )。
A.钝角三角形 B.锐角三角形 C.直角三角形 D.无法确定
8.如图,甲与乙的周长相比,( )。
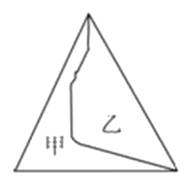
A.甲的周长>乙的周长 B.甲的周长<乙的周长 C.甲的周长=乙的周长 D.无法比较
二、填空题(26分)
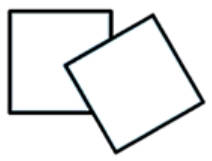
9.如图,有两个边长是6厘米的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积是( )平方厘米。
10.将一个长方体的高增加3厘米后变成一个正方体,它的表面积比原来增加84平方厘米,原来长方体的体积是( )立方厘米。
11.在一幅比例尺为1∶3000的图纸上,量得一个三角形菜地的底是20厘米,高15厘米,这块菜地的实际面积是( )公顷。
12.一顶帽子,上面是直径2dm,高1dm的圆柱形(有帽顶),帽檐部分是一个宽1dm的圆环,做这顶帽子,至少要用( )的布料。(接头处忽略不计)
13.一根圆柱形木料,长3米,平均截成2段以后,表面积增加了18.84平方分米,原来这根木料的体积是( )立方分米。
14.两个长方形,长都是8厘米,宽都是4厘米,把它们拼成一个长方形,周长是( )厘米;如果把它们拼成一个正方形,周长是( )厘米。
15.一个圆柱和一个圆锥高相等,体积的比是6∶1,如果圆柱的底面积是3.6平方分米,圆锥的底面积是( )平方分米。
16.已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是( )cm。
17.一根圆柱形木料,底面直径是20厘米,长是1.8厘米。把它截成6段同样的小圆柱,截开后,表面积增加了( )平方厘米[π取3]。
18.用5个大小相等的小正方体搭成下面三个立体图形,从( )面看这三个立体图形所看到的形状是完全一样的。
19.有一张长9.42米,宽4米的长方形铁皮,把它卷成一个最大的圆柱体,这个圆柱体的侧面积是( )平方米,把圆柱竖着放,占地( )平方米。
20.一个圆柱与圆锥的体积相等,圆柱的底面半径是圆锥的,已知圆锥的高是36厘米,圆柱的高是( )厘米。
三、判断题(10分)
21.用圆柱体侧面积的一半乘底面半径等于这个圆柱的体积。( )
22.从新华书店至公园是向北偏东50°方向行驶1.5千米,返回时应向南偏西40°方向行驶1.5千米。( )
23.长度分别是5cm、3cm、8厘米的三根小棒,可以围成一个三角形。( )
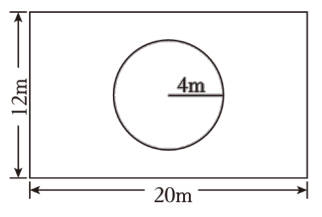
24.笑笑量出自己的步长约为5分米,她沿操场走了一圈,共走了820步,操场一圈大约为500米。( )
25.观察课桌,站在不同的位置最多能看到2个面。( )
四、图形计算(12分)
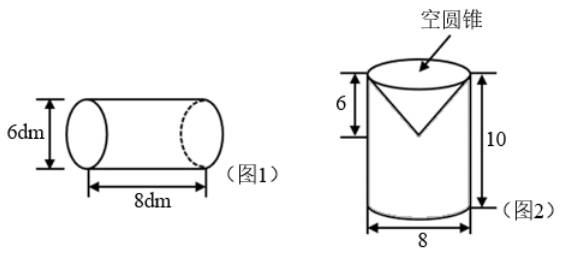
26.求下面图1的表面积,图2的体积。(图2单位:cm)
27.求下面圆柱和圆锥的体积。

五、作图题(12分)
28.在下面的方格图上按要求画图。(每个小方格的边长表示1cm)
①画一个周长20厘米,长和宽的比是3∶2的长方形。
②将所画长方形的面积按2∶1分成两部分,其中面积较小的一部分画上斜线。

29.下面每个小方格都代表边长1厘米的正方形,按要求画一画。
(1)在下图的长方形中涂上红色与黑色,且红色格子与黑色格子的面积比是5∶2。
(2)画一个周长是32厘米的长方形,且长与宽的比是5∶3。

30.画出各景点的位置。
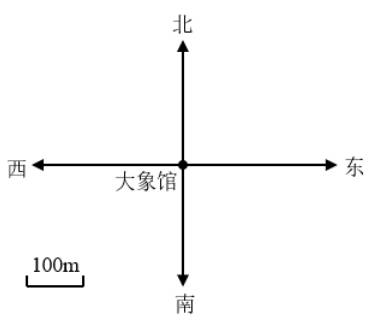
(1)鳄鱼潭在大象馆西偏北40°方向100米处。
(2)熊猫馆在大象馆南偏东70°方向400米处。
(3)狮虎山在大象馆东偏北30°方向300米处。
31.画出下面立体图形从正面、上面、左面看到的形状。

六、解答题(24分)
32.如图所示,这是一块长方形草坪,中间有一个圆形花坛。这块草坪的面积是多少平方米?
33.按要求完成下面各题。
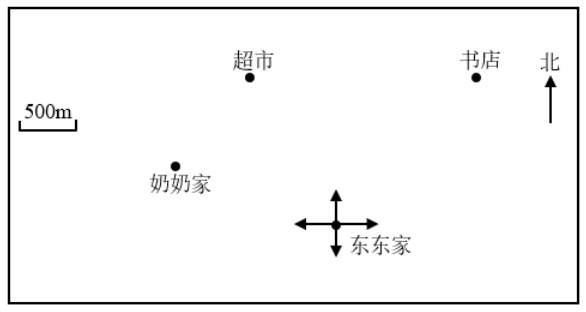
(1)东东骑车从家出发,经过超市,再去书店。他骑车的速度是250米/分,途中需要多少分钟?请你先在图中画一画,再算一算。
(2)东东买完书后,先去超市买东西,然后去看望奶奶。请你写出东东从书店去奶奶家的路线。
34.下面是一个圆柱的表面展开图,这个圆柱的表面积是多少平方厘米?体积是多少立方厘米?
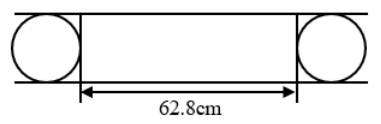
35.一个直径是8厘米,高是10厘米的圆柱体,往里面加入6厘米深的水。将一个圆锥体放进去,水溢出9.42立方厘米。这个圆锥的体积是多少立方厘米?
36.张大伯新建一个圆柱形水池(无盖),底面直径8米,池深2米。
①这个水池的占地面积是多少平方米?
②如果在水池的底面和四周做一层新型的防渗水涂料,涂料每平方米的造价为20元,张大伯最少要付多少元?
③这个水池的容积是多少立方米?
37.学校新建一排球场地,长是18米,宽是9米,请按1∶300的比例尺画在图纸上,这个排球场的平面图面积是多少?
38.一个圆柱形储油罐,从里面量,底面直径是2米,高是4米,如果1升汽油重0.75千克,这个储油罐最多可装汽油多少千克?
39.一个圆锥形麦堆,底面直径6米,高0.9米,每立方米小麦约重500千克,这堆小麦重多少千克?若把这些小麦加工成面粉,小麦的出粉率是80%,可以加工面粉多少千克?
1.D
【分析】根据容积的意义,某容器所能容纳别的物体的体积叫做容器的容积。据此解答。
【详解】计算鱼缸能装水多少升,是求鱼缸的容积。
故答案为:D
【点睛】本题考查的目的是理解掌握容积的意义及应用。
2.C
【分析】已知小明每天用底面直径6cm,高10cm的圆柱形水杯喝水,根据圆柱的体积公式V=πr2h,以及进率“1cm3=1mL”,求出水杯的容积;
再用要求儿童每天喝水的至少摄入量除以水杯的容积,商采用“进一法”取整数,即是小明每天至少要喝的杯数。
【详解】3.14×(6÷2)2×10
=3.14×9×10
=282.6(cm3)
282.6cm3=282.6mL
1500÷282.6≈6(杯)
至少喝水6杯。
故答案为:C
【点睛】本题考查圆柱体积公式的运用以及体积、容积单位的换算,注意求至少要喝的杯数时,计算结果采用“进一法”取整数。
1.计算鱼缸能装水多少升,是求鱼缸的( )。
A.表面积 B.棱长总和 C.体积 D.容积
2.营养学家建议:儿童每天水的摄入量应不少于1500mL。要达到这个要求,小明每天用底面直径6cm,高10cm的圆柱形水杯喝水,至少喝水( )杯。
A.4 B.5 C.6 D.7
3.两个圆柱形容器内原来的水面高度都是6cm。它们的底面直径都是10cm。①号容器内放入一个小球后,水面高度为10cm。②号容器内放入一个小球和一个大球,水面高度为16cm。两个容器内的小球完全相同,水也均未溢出,小球的体积与大球的体积的比是( )。
A.5∶8 B.2∶5 C.2∶3 D.5∶12
4.制作一个无盖的圆柱形容器,应该选择( )。

A.①和③ B.①和④ C.②和③ D.②和④
5.下面各图中,( )是不正确的。

6.如图是由7个立方体摆成的几何体,从右面观察到的图形是( )。
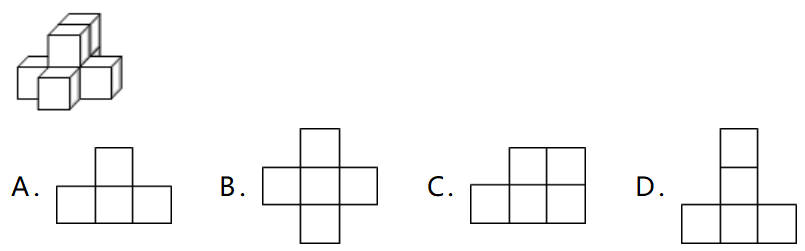
7.一个三角形,三个内角度数比是2∶3∶1,这个三角形按角分是( )。
A.钝角三角形 B.锐角三角形 C.直角三角形 D.无法确定
8.如图,甲与乙的周长相比,( )。

A.甲的周长>乙的周长 B.甲的周长<乙的周长 C.甲的周长=乙的周长 D.无法比较
二、填空题(26分)
9.如图,有两个边长是6厘米的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,重叠部分的面积是( )平方厘米。

10.将一个长方体的高增加3厘米后变成一个正方体,它的表面积比原来增加84平方厘米,原来长方体的体积是( )立方厘米。
11.在一幅比例尺为1∶3000的图纸上,量得一个三角形菜地的底是20厘米,高15厘米,这块菜地的实际面积是( )公顷。
12.一顶帽子,上面是直径2dm,高1dm的圆柱形(有帽顶),帽檐部分是一个宽1dm的圆环,做这顶帽子,至少要用( )的布料。(接头处忽略不计)
13.一根圆柱形木料,长3米,平均截成2段以后,表面积增加了18.84平方分米,原来这根木料的体积是( )立方分米。
14.两个长方形,长都是8厘米,宽都是4厘米,把它们拼成一个长方形,周长是( )厘米;如果把它们拼成一个正方形,周长是( )厘米。
15.一个圆柱和一个圆锥高相等,体积的比是6∶1,如果圆柱的底面积是3.6平方分米,圆锥的底面积是( )平方分米。
16.已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是( )cm。
17.一根圆柱形木料,底面直径是20厘米,长是1.8厘米。把它截成6段同样的小圆柱,截开后,表面积增加了( )平方厘米[π取3]。
18.用5个大小相等的小正方体搭成下面三个立体图形,从( )面看这三个立体图形所看到的形状是完全一样的。

19.有一张长9.42米,宽4米的长方形铁皮,把它卷成一个最大的圆柱体,这个圆柱体的侧面积是( )平方米,把圆柱竖着放,占地( )平方米。
20.一个圆柱与圆锥的体积相等,圆柱的底面半径是圆锥的,已知圆锥的高是36厘米,圆柱的高是( )厘米。
三、判断题(10分)
21.用圆柱体侧面积的一半乘底面半径等于这个圆柱的体积。( )
22.从新华书店至公园是向北偏东50°方向行驶1.5千米,返回时应向南偏西40°方向行驶1.5千米。( )
23.长度分别是5cm、3cm、8厘米的三根小棒,可以围成一个三角形。( )
24.笑笑量出自己的步长约为5分米,她沿操场走了一圈,共走了820步,操场一圈大约为500米。( )
25.观察课桌,站在不同的位置最多能看到2个面。( )
四、图形计算(12分)
26.求下面图1的表面积,图2的体积。(图2单位:cm)

27.求下面圆柱和圆锥的体积。

五、作图题(12分)
28.在下面的方格图上按要求画图。(每个小方格的边长表示1cm)
①画一个周长20厘米,长和宽的比是3∶2的长方形。
②将所画长方形的面积按2∶1分成两部分,其中面积较小的一部分画上斜线。

29.下面每个小方格都代表边长1厘米的正方形,按要求画一画。
(1)在下图的长方形中涂上红色与黑色,且红色格子与黑色格子的面积比是5∶2。
(2)画一个周长是32厘米的长方形,且长与宽的比是5∶3。

30.画出各景点的位置。

(1)鳄鱼潭在大象馆西偏北40°方向100米处。
(2)熊猫馆在大象馆南偏东70°方向400米处。
(3)狮虎山在大象馆东偏北30°方向300米处。
31.画出下面立体图形从正面、上面、左面看到的形状。

六、解答题(24分)
32.如图所示,这是一块长方形草坪,中间有一个圆形花坛。这块草坪的面积是多少平方米?

33.按要求完成下面各题。

(1)东东骑车从家出发,经过超市,再去书店。他骑车的速度是250米/分,途中需要多少分钟?请你先在图中画一画,再算一算。
(2)东东买完书后,先去超市买东西,然后去看望奶奶。请你写出东东从书店去奶奶家的路线。
34.下面是一个圆柱的表面展开图,这个圆柱的表面积是多少平方厘米?体积是多少立方厘米?

35.一个直径是8厘米,高是10厘米的圆柱体,往里面加入6厘米深的水。将一个圆锥体放进去,水溢出9.42立方厘米。这个圆锥的体积是多少立方厘米?
36.张大伯新建一个圆柱形水池(无盖),底面直径8米,池深2米。
①这个水池的占地面积是多少平方米?
②如果在水池的底面和四周做一层新型的防渗水涂料,涂料每平方米的造价为20元,张大伯最少要付多少元?
③这个水池的容积是多少立方米?
37.学校新建一排球场地,长是18米,宽是9米,请按1∶300的比例尺画在图纸上,这个排球场的平面图面积是多少?
38.一个圆柱形储油罐,从里面量,底面直径是2米,高是4米,如果1升汽油重0.75千克,这个储油罐最多可装汽油多少千克?
39.一个圆锥形麦堆,底面直径6米,高0.9米,每立方米小麦约重500千克,这堆小麦重多少千克?若把这些小麦加工成面粉,小麦的出粉率是80%,可以加工面粉多少千克?
参考答案
1.D
【分析】根据容积的意义,某容器所能容纳别的物体的体积叫做容器的容积。据此解答。
【详解】计算鱼缸能装水多少升,是求鱼缸的容积。
故答案为:D
【点睛】本题考查的目的是理解掌握容积的意义及应用。
2.C
【分析】已知小明每天用底面直径6cm,高10cm的圆柱形水杯喝水,根据圆柱的体积公式V=πr2h,以及进率“1cm3=1mL”,求出水杯的容积;
再用要求儿童每天喝水的至少摄入量除以水杯的容积,商采用“进一法”取整数,即是小明每天至少要喝的杯数。
【详解】3.14×(6÷2)2×10
=3.14×9×10
=282.6(cm3)
282.6cm3=282.6mL
1500÷282.6≈6(杯)
至少喝水6杯。
故答案为:C
【点睛】本题考查圆柱体积公式的运用以及体积、容积单位的换算,注意求至少要喝的杯数时,计算结果采用“进一法”取整数。
更多答案请自行下载免费文档(文档正规渠道存储,请放心下载)
