注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.4a+8错写成4×(a+8),结果比原来( )。
A.多4 B.少4 C.多24
2.一块半圆铁片,半径是r,它的周长是( )。
A.πr B.πr+r C.πr+2r
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.4a+8错写成4×(a+8),结果比原来( )。
A.多4 B.少4 C.多24
2.一块半圆铁片,半径是r,它的周长是( )。
A.πr B.πr+r C.πr+2r
3.一根电线,截去了后,还剩下m,截去的和剩下的相比,( )。
A.截去的短 B.截去的长 C.一样长
4.一个长、宽与高都是的长方体,将它挖掉一个棱长的小正方体后(如图),它的表面积( )。
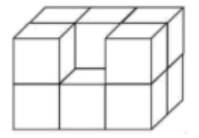
A.比原来大 B.比原来小 C.不变
5.下面说法中,正确的是( )。
A.圆的半径和它的面积成正比例关系。
B.用长、、的三条线段可以围成一个三角形。
C.把一个正方形按4∶1放大,放大后的图形面积是原来的16倍。
二、填空题
6.国家雪车雪撬中心是北京冬奥会雪车、雪撬、钢架雪车项目的比赛场地,建筑面积52500平方米,横线上的数读作( ),省略万后面的尾数约是( )万平方米。
7.如果规定向东为正,那么向东走8m记作﹢8m,﹣6m表示( )。
8.4/( )=0.2=( )∶5=( )%=( )折。
9.如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是( ),最小公倍数是( )。
10.统计某地区一周气温的变化情况,用( )统计图比较合适;描述牛奶中各成分的组成情况,用( )统计图比较合适。
11.大小两个圆的半径之比是2∶1,它们的直径之比是( ),周长之比( ),面积之比是( )。
12.黄叔叔存入银行50000元,定期两年,年利率是2.1%,到期可得到利息( )元。
13.等底等高的圆柱和圆锥体积差为62.8cm3,圆锥的体积是( )cm3,圆柱的体积是( ) cm3。
三、判断题
14.5m的1/6与6m的1/5一样长。( )
15.一个圆柱的体积是21立方分米,那么圆锥的体积是7立方分米。( )
16.甲数和乙数的比是4∶5,那么乙数比甲数多25%。( )
17.把32个篮球分给6个小组,总有1个小组至少分到6个篮球。( )
18.一个圆柱的底面半径扩大3倍,高不变,体积扩大6倍。( )
四、计算题
19.直接写出得数。
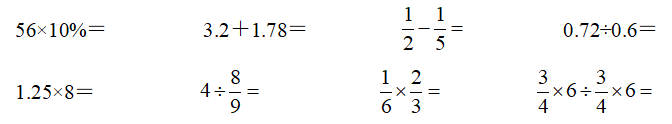
20.计算下面各题,怎样简便就怎样算。
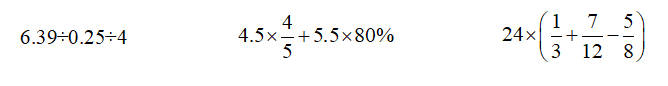
21.求未知数。

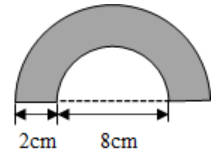
22.如图:求阴影部分的面积。
五、解答题
23.中国古代《孙子算经》共三卷,成书大约在公元5世纪。这本书浅显易懂,有许多有趣的算术题,比如“鸡兔同笼”问题:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?(雉俗称“野鸡”)
24.采石场爆破时,点燃导火线后工人要在爆破前转移到200米外的安全区域,导火线燃烧速度是1.2厘米/秒,工人转移的速度是5米/秒,考虑到撤离中可能出现的意外还要留有10秒的安全保障时间,请问这次爆破至少要准备多少厘米的导火索才能确保爆破人员安全撤离?
25.学校原有足球、篮球共54个,其中足球与篮球个数的比是4∶5,本月买进一些篮球后,足球个数占足球、篮球总个数的40%,现在学校的足球、篮球各有多少个?
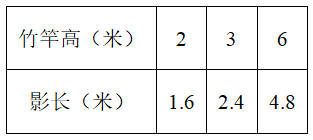
26.同一时间,同一地点测得竹竿高度及其影长如下表。如果竹竿高是8米,你能计算出它的影长吗?(用比例解答)
27.一个粮仓(如图),如果每立方米粮食重600千克,这个粮仓大约能装多少千克粮食?(结果保留整数)

28.心灵手巧,我会做。(请用2B铅笔在答题卡上绘图,图案要绘制清晰。)
下图每个小方格的边长是1厘米,请按要求完成下列各题。
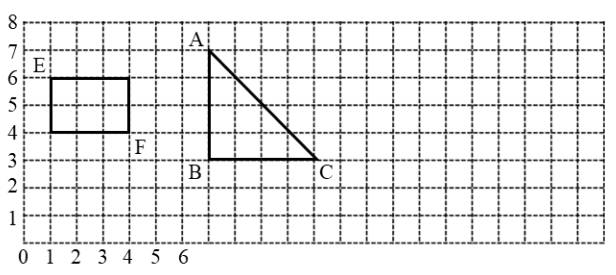
(1)把图中的长方形绕点F顺时针旋转90º,画出旋转后的图形。E点旋转后的位置用数对表示是( )。
(2)按1∶2的比画出△ABC缩小后的图形。
(3)在△ABC中,C点在A点( )偏( )( )º方向。
(4)请在方格上画一个面积是8平方厘米的梯形。
参考答案
1.C
【分析】将算式4(a+8)去括号,计算出结果,再求与4a+8的差即可。
【详解】4(a+8)-(4a+8)
=4a+32-4a-8
=32-8
=24
则结果比原来多24。
故答案为:C
【点睛】本题考查了用乘法分配律计算含字母的算式,要熟记运算律并能灵活使用。
2.C
【分析】根据半圆的周长=整圆的周长的一半+一条直径的长度,据此解答即可。
【详解】2πr÷2+2r=πr+2r
则它的周长是πr+2r。
故答案为:C
【点睛】本题考查圆的周长,明确半圆的周长的计算方法是解题的关键。
3.A
【分析】根据题意,把这一根电线的全长看作单位“1”,平均分成5段,其中截去其中的2段,那么剩下的有(5-2)段,也就是占全长的,长米,比较两个分数的大小即可。
【详解】解:1-=
因为,所以剩下的长,截去的短。
故答案为:A
【点睛】解答此题的关键是理解两个分数的不同表示意义。
4.A
【分析】由题意可知,将这个长方体挖掉一个小正方体后,表面积减少了2个正方形的面积,但又增加了4个正方形的面积,所以挖掉一个小正方体后的长方体比原来的长方体的表面积增加了2个正方形的面积。
【详解】由分析可知:
将它挖掉一个棱长的小正方体后(如图),它的表面积比原来大。
故答案为:A
【点睛】本题考查长方体的表面积,明确表面积的定义是解题的关键。
5.C
【分析】A.判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例;如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
B.能组成三角形,三条边必须要符合三边关系:在一个三角形中,任意两边之和大于第三边。
C.根据正方形的面积=边长×边长,以及积的变化规律可知,把一个正方形按4∶1放大,放大后的图形面积是原来的(4×4)倍。
【详解】A.根据圆的面积公式S=πr2可知,S÷r=πr(不一定),所以圆的半径和它的面积不成比例,原题说法错误。
B.4+9=13,所以用长、、的三条线段不能围成一个三角形,原题说法错误;
C.4×4=16
把一个正方形按4∶1放大,放大后的图形面积是原来的16倍,原题说法正确。
故答案为:C
【点睛】掌握正、反比例的意义及辨识方法、三角形的三边关系、图形的放大、正方形的面积公式是解题的关键。
6. 五万二千五百 5
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;改写成用“万”作单位的数,根据千位上的数字进行四舍五入。
【详解】52500读作:五万二千五百
52500≈5万
【点睛】本题主要考查整数的读法和改写。分级读即可快速、正确地读出此数;改写时要带计数单位。
7.向西走6m
【分析】用正负数表示意义相反的两种量:向东走记作正,则向西走就记作负。由此得解。
【详解】向东走8m记作﹢8m,﹣6m表示向西走6m。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,和它意义相反的就为负。
8.20;1;20;二
【分析】把0.2化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据比与分数的关系,=1∶5;把0.2的小数点向右移动两位添上百分号就是20%;根据折扣的意义,20%就是二折。
【详解】=0.2=1∶5=20%=二折
【点睛】此题主要是考查小数、分数、百分数、比、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
9. b a
【分析】两数成倍数关系,最大公因数是较小数,最小公倍数是较大数,据此分析。
【详解】如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是b,最小公倍数是a。
【点睛】特殊情况还有两数互质,最大公因数是1,最小公倍数是两数的积。
10. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此解答即可。
【详解】统计某地区一周气温的变化情况,用折线统计图比较合适;描述牛奶中各成分的组成情况,用扇形统计图比较合适。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
更多答案请自行下载免费文档(文档正规渠道存储,请放心下载,免费下载)
