一、选择题（每小题1分，共6分）
1．两数相除的商是9.05，如果被除数扩大为原来的10倍，除数缩小到原来的 1/100，那么商是（ ）
A．0.905 B．90.5 C．905.0 D．9050
2．一个两位小数取进似值保留一位小数是6.0，这个两位小数是（ ）
A．5.59 B．5.94 C．6.04 D．6.08
3．面图形中，对称轴最多的是（ ）
4．已知12□4是3的倍数，□中的数字共有（ ）种填法。
A．1 B．2 C．3 D．4
5．下面的四句话中，说法正确的是（ ）
A．最小的合数是2 B．所有的偶数都是合数
C．所有的奇数都是质数 D．1既不是质数，也不是合数
6．用四根木条钉成一个长方形框架，长是20厘米，宽是12厘米，如果把它拉成一个平行四边形框架，这个平行四边形的面积（ ）240平方厘米。
A．大于 B．小于 C．等于 D．无法确定
二、填空题（每空1分，共28分）
7．甜甜计算一道除法算式时，错把被除数39.6写成了36.9，结果商正好比原来小了1.2，正确的商是( )
8．在括号里填上“＞”“＜”或“＝”
6.42( )6.424 5.62÷0.97( )5.62 4.5÷1.01( )4.5÷0.99
9．每个油瓶最多能装2.3kg油，要装45kg油，至少需要这样的油瓶( )个；13m的布，每2.4m做一套衣服，最多可以做( )套。
10．19.282828…，可以简写作( )，它的循环节是( )，保留两位小数约是( )
11．2024年5月19日，1港元兑换人民币0.87元，笑笑这天用100元人民币能兑换( )港元。（结果保留两位小数）
12．平移改变的是图形的( )，图形的( )和( )不变。
13．
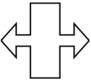有( )条对称轴。
有( )条对称轴。 14．在算式25×3＝75中，( )是( )的倍数，( )是( )的因数。
15．11～18中，合数有( )个，质数有( )个，2的倍数有( )个。
16．两个质数的和是22，积是85，这两个质数分别是( )、( )
17．一个平行四边形面积是4.6平方米，它的底是8米，这个平行四边形底对应的高是( )
18．一个等边三角形的周长是15cm，高是2.4cm，它的面积是( )cm2
19．一个平行四边形的底是10厘米，高是3.6厘米，面积是( )平方厘米。和它等底等高的三角形的面积是( )平方厘米。
20．一个梯形的面积为48.6dm2，上、下底的和为10.8dm，则这个梯形的高为( )dm
三、判断题（每小题1分，共6分）
21．不是所有的无限小数都比有限小数大。( )
22．一个数（0除外）除以0.01，就是把这个数扩大到原来的10倍。( )
23．钟表上的指针都做平移运动。( )
24．如果一个数的因数中有6，那么这个数一定是6的倍数。( )
25．如果a是奇数，那么a＋2的结果还是奇数。( )
26．如果两个平行四边形的面积相等，那么这两个平行四边形的底和高也分别相等。( )
四、计算题（27小题8分，28小题9分，29小题3分，30小题6分。共32分）
27．直接写出得数。
6.85÷10＝ 4.2÷0.06＝ 3.9÷1.3＝ 7.2÷24＝
0.4÷0.8＝ 0.64÷2＝ 9.5÷0.5＝ 4.5÷0.03＝
28．竖式计算。
0.48÷3.2＝ 3.05÷0.89≈（得数保留一位小数） 18÷4.4＝（商用循环小数表示）
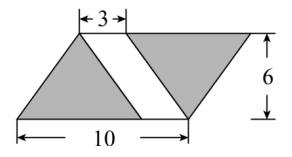
29．求下图阴影部分的面积。（单位：厘米）
30．计算下面图形的面积。（单位：米）
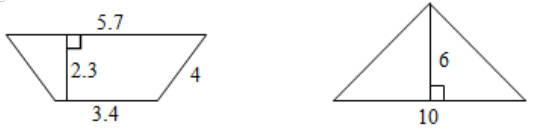
五、作图题（每小题4分，共8分）
31．画一画。
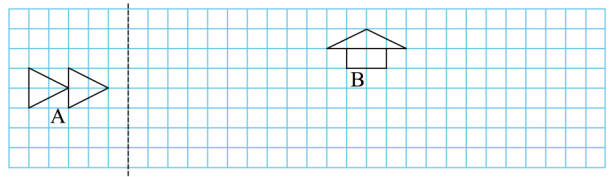
（1）以虚线为对称轴，画出图形A的轴对称图形。
（2）画出图形B先向下平移3格，再向右平移4格后的图形。
32．画出各图形指定底边的高。
六、解答题（第33、34小题各4分，其余每小题5分，共28分）
33．每个油桶最多可装3.6千克油，装20千克油至少需要几个这样的油桶？
34．一间教室的面积是46.35平方米，用面积是0.25平方米的正方形瓷砖铺地，共需这种瓷砖多少块？
35．李叔叔暑假从西安到兰州自驾游。去时平均每时行驶96千米，用了7时到达，返回时平均每时行驶80千米，返回时用了多长时间？
36．水果店运进苹果和香蕉共250千克，苹果的质量是香蕉的1.5倍多20千克。运进苹果和香蕉各多少千克？
37．学校有一块平行四边形菜地，底是25米，高是12米。如果在这块菜地里种茄子，平均每平方米可以种2.5棵茄苗，一共可以种多少棵茄苗？
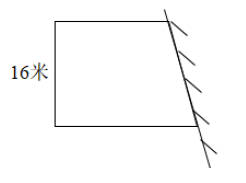
38．王大爷用85米长的篱笆围成一个梯形，一边靠墙（如图），求该梯形的面积。
参考答案
1．D
【分析】根据商的变化规律，被除数扩大为原来的几倍，商扩大为原来的几倍，除数缩小到原来的几分之一，商反而扩到原来的几倍，据此分析。
【详解】9.05×10×100＝9050
商是9050。
故答案为：D
2．C
【分析】两位小数若通过“四舍”取进似值保留一位小数是6.0，则原数可能是6.01、6.02、6.03、6.04。若通过“五入”取进似值保留一位小数是6.0，则原数可能是5.95、5.96、5.97、5.98、5.99。据此解答。
【详解】根据分析，原数可能是5.95、5.96、5.97、5.98、5.99、6.01、6.02、6.03、6.04。所以题目中的两位小数是6.04。
故答案为：C
3．D
【分析】把一个图形沿某条直线对折后，图形的两部分能够完全重合，那么这样的图形就被称为轴对称图形，这条直线就是它的对称轴，据此解答。
【详解】
如图所示，有2条对称轴，有4条对称轴，有3条对称轴，有5条对称轴。
故答案为：D
4．C
【分析】3的倍数特征：各个数位上的数字和是3的倍数；据此判断即可。
【详解】1＋2＋4＝7
比7大的3的倍数有：9、12、15、18…
9－7＝2
12－7＝5
15－7＝8
18－7＝11
……
因为□中的数字不能超过9，所以□只能填2、5、8，一共3种填法。
故答案为：C
5．D
【分析】质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数；合数是指在大于1的自然数中，除了1和它本身以外，还有其他因数的数；1既不是质数，也不是合数；是2的倍数的数，叫做偶数；不是2的倍数的数，叫做奇数。据此逐项分析即可解答。
【详解】A．最小的合数是4，原题说法错误；
B．2是偶数不是合数，原题说法错误；
C．1是奇数，不是质数，原题说法错误；
D．1既不是质数，也不是合数，原题说法正确。
故答案为：D
6．B
【分析】平行四边形面积＝底×高，长方形面积＝长×宽，分析长方形的长和宽与平行四边形的底和高之间的关系，即可得出结论。
【详解】20×12＝240（平方厘米）
长方形拉成一个平行四边形，长方形的长＝平行四边形的底，长方形的宽＞平行四边形的高，长×宽＞底×高，即平行四边形面积＜长方形面积，这个平行四边形的面积小于240平方厘米。
故答案为：B
7．17.6
【分析】当除数不变时，被除数越少，商越少，把39.6错写成36.9，被除数少了39.6－36.9＝2.7，根据“除数＝被除数的变化量÷商的变化量”求出除数，再求商。
【详解】（39.6－36.9）÷1.2
＝2.7÷1.2
＝2.25
39.6÷2.25＝17.6
所以正确的商是17.6。
8．＜ ＞ ＜
【分析】第一小题：根据小数比较大小的方法：先看整数部分，整数部分大的那个数就大；如果整数部分相同，就看十分位上的数，十分位上的数大的那个数就大；如果十分位上的数也相同，就看百分位上的数，百分位上的数大的那个数就大，依此类推，进行解答。
第二、三小题：一个非0数，除以大于1的数，商小于被除数；一个非0数，除以小于1的数，商大于被除数，据此解答。
【详解】6.42和6.424
6.42＜6.424
5.62÷0.97和5.62
因为0.97＜1，所以5.62÷0.97＞5.62
4.5÷1.01和4.5÷0.99
因为1.01＞1，所以4.5÷1.01＜4.5
因为0.99＜1，所以4.5÷0.99＞4.5，因此4.5÷1.01＜4.5÷0.99
9．20 5
【分析】①用油的总重量45kg除以每个油瓶能装的最多的油的重量2.3kg，不够一瓶也需要一瓶装，则适用“进一法”取值，即可求出至少需要这样的油瓶几个；
②用布的总米数13m除以每套衣服用的米数2.4m，不够一套衣服的布料需要舍去，则适用“去尾法”取值，即可求出最多可以做几套。
【详解】①45÷2.3≈19.6≈20（个），即至少需要这样的油瓶20个；
②（套），即最多可以做5套。
10．19.282828… 28 19.28
【分析】循环小数的简写方法是在循环节的首位和末位数字上面各记一个小圆点。对于19.282828…，其循环节是“28”，所以可以简写作19.282828…。循环节是指一个循环小数的小数部分依次不断的重复出现的一个或几个数字，所以该数的循环节是28。保留两位小数，需要看小数点后第三位数字，如大于等于5，则向前进1，如小于5则舍去；19.282828…的小数点后第三位是2，2＜5，舍去，所以保留两位小数约是19.28。
11．114.94
【分析】求100元人民币可以兑换多少港元，就是求100里面有多少个0.87，用除法计算。保留两位小数，看小数点后的第三位，如果小数点后的第三位大于等于5，则进一，小于5，则舍去。
【详解】100÷0.87≈114.94（港元）
笑笑这天用100元人民币能兑换114.94港元。
12．位置 大小 形状
【分析】在平面内，把一个图形整体沿某条直线方向平行移动一定距离的过程，称为平移，把一个图形平移之后会得到一个新的图形，新图形与原图形的形状和大小完全相同，所以平移只是图形的位置发生了变化，形状和大小没有发生变化，据此解答。
【详解】分析可知，平移改变的是图形的位置，图形的大小和形状不变。
13．2
【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后，两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，据此解答。
【详解】
如图：2条对称轴。
14．75 25和3 25和3 75
【分析】若整数a能够被b整除，如：a÷b＝c，a是 b和c的倍数，b和c是a的因数，因数与倍数是相互依存的。
【详解】在算式25×3＝75中，75是25和3的倍数，25和3是75的因数；或75是3和25的倍数，3和25是75的因数。
15．5 3 4
【分析】一个数，如果只有1和它本身两个因数，这样的数叫做质数；一个数，如果除了1和它本身还有别的因数，这样的数叫做合数；2的倍数的特征：个位是0、2、4、6、8的数。据此解答。
【详解】在11～18中：
11的因数，有1和11，所以11是质数；
12的因数有1、2、3、4、6、12，所以12是合数，12的个位是2，所以12也是偶数；
13的因数有1和13，所以13是质数；
14的因数有1、2、7、14，所以14是合数，14的个位是4，所以14也是偶数；
15的因数有1、3、5、15，所以15是合数；
16的因数有1、2、4、8、16，所以16是合数，16的个位是6，所以16也是偶数；
17的因数有1和17，所以17是质数；
18的因数有1、2、3、6、9、18，所以18是合数，18的个位是8，所以18也是偶数。
所以11～18中，合数有12、14、15、16、18，共5个，质数有11、13、17，共3个，2的倍数有12、14、16、18，共4个。
16．5 17
【分析】一个数，如果只有1和它本身两个因数，这样的数叫作质数，最小的质数是2，据此列出和为22的质数对，再验证它们的积是否为85。
【详解】3＋19＝22，3×19＝57≠85，不符合题意，舍去；
5＋17＝22，5×17＝85，符合题意；
11＋11＝22，11×11＝121≠85，不符合题意，舍去。
所以这两个质数分别是5和17。
17．0.575米/0.575m
【分析】根据平行四边形的面积÷底＝高，用4.6÷8即可求出这个平行四边形底对应的高。
【详解】4.6÷8＝0.575（米）
这个平行四边形底对应的高是0.575米。
18．6
【分析】将等边三角形的周长除以3，求出它的边长，即底。再根据三角形面积＝底×高÷2，将数据代入公式，求出这个三角形的面积。
【详解】15÷3＝5（cm）
5×2.4÷2
＝12÷2
＝6（cm2）
则它的面积是6cm2。
19．36 18
【分析】平行四边形面积＝底×高，三角形面积＝底×高÷2，据此列式求出这个平行四边形和三角形的面积。
【详解】10×3.6＝36（平方厘米）
10×3.6÷2
＝36÷2
＝18（平方厘米）
所以，这个平行四边形的面积是36平方厘米，和它等底等高的三角形的面积是18平方厘米。
【点睛】本题考查了平行四边形和三角形的面积，熟记面积公式是解题的关键。
20．9
【分析】根据梯形的面积公式： 梯形面积＝（上底＋下底）×高÷2，推导出已知梯形面积、上下底之和时求梯形的高的公式为：高＝梯形面积×2÷（上底＋下底），据此得出答案。
【详解】48.6×2÷10.8
＝97.2÷10.8
＝9（dm）
所以这个梯形的高为9dm。
【点睛】考查了学生对梯形的面积的理解和应用能力。
21．√
【分析】无限小数包括无限循环小数和无限不循环小数，有限小数是小数点后位数有限的小数。例如，无限小数0.333…小于有限小数0.4，说明并非所有无限小数都比有限小数大。
【详解】例如：无限小数0.333…，有限小数0.4。
0.333…＜0.4
因此存在无限小数比有限小数小的情况，原说法正确。
故答案为：√
22．×
【分析】一个数（0除外）除以0.01，小数点向右移动两位即可，相当于将其转化为乘100，因此这个数会扩大到原来的100倍，举例说明即可。
【详解】2÷0.01＝200，200是2的100倍。一个数（0除外）除以0.01，就是把这个数扩大到原来的100倍，原题说法错误。
故答案为：×
23．×
【分析】在平面内，把一个图形整体沿某条直线方向平行移动一定距离的过程，称为平移；在平面内，把一个图形围绕某一固定点按顺时针或者逆时针的方向转动一定角度的过程，称为旋转，据此解答。
【详解】分析可知，钟表上的指针都做旋转运动，而不是平移运动，题目说法错误。
故答案为：×
24．√
【分析】如果整数a除以整数b（b≠0）的商是整数且没有余数，就说a是b的倍数，b是a的因数。若一个数的因数中有6，则这个数能被6整除，因此，该数一定是6的倍数。
【详解】一个数的因数中有6，这个数能被6整除，该数一定是6的倍数。原说法正确。
故答案为：√
25．√
【分析】奇数是不能被2整除的整数，偶数是能被2整除的数。根据奇数和偶数的运算性质，奇数与偶数相加的结果为奇数。题目中a是奇数，2是偶数，因此a＋2的结果应为奇数。
【详解】奇数＋偶数＝奇数
a＋2的结果是奇数，原说法正确。
故答案为：√
26．×
【分析】平行四边形面积＝底×高，面积相等的两个平行四边形，底和高不一定相等，举例说明即可。
【详解】如果两个平行四边形的面积相等，那么这两个平行四边形的底和高不一定相等。
如：6×2＝12（平方厘米）
4×3＝12（平方厘米）
一个平行四边形的底6厘米，高2厘米，另一个平行四边形的底4厘米，高3厘米，面积都是12平方厘米。
故答案为：×
27．0.685；70；3；0.3
0.5；0.32；19；150
28．0.15；3.4；
【分析】除数是小数的除法计算法则：先移动除数的小数点，使它变成整数，被除数的小数点也向右移动几位（位数不够的补“0”），然后按照除数是整数的除法法则进行计算；
保留几位小数，就看保留小数的下一位小数，再根据“四舍五入”法进行解答；
写循环小数时，可以只写第一个循环节，并在这个循环节的首位和末位数字上面各记一个圆点。
【详解】0.48÷3.2＝0.15 3.05÷0.89≈3.4 18÷4.4＝
29．42平方厘米
【分析】由图可知，阴影部分的面积可以看成是一个底为10厘米，高为6厘米的平行四边形的面积去掉一个底为3厘米，高为6厘米的平行四边形的面积，平行四边形的面积＝底×高，代入数据计算即可。
【详解】10×6－3×6
＝60－18
＝42（平方厘米）
阴影部分的面积是42平方厘米。
30．10.465平方米；30平方米
【分析】根据梯形的面积公式：（上底＋下底）×高÷2，三角形的面积公式：底×高÷2，把数代入即可求解。
【详解】梯形面积：（3.4＋5.7）×2.3÷2
＝9.1×2.3÷2
＝20.93÷2
＝10.465（平方米）
三角形面积：10×6÷2
＝60÷2
＝30（平方米）
31．【分析】（1）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左图A的关键对称点，依次连接即可。
（2）根据平移的特征，把图B的各顶点分别向下平移3格，再向右平移4格，依次连接即可得到平移后的图形。
【详解】（1）图形A的轴对称图形如图所示：
（2）图形B先向下平移3格，再向右平移4格后的图形如图所示：
32．【分析】从平行四边形的一条边上的任意一点都可以向对边作垂直线段，即是平行四边形的高；从三角形底边对应顶点做底边或者底边的延长线的垂线，从顶点到垂足间的线段叫做三角形的高。
【详解】画图如下：
【点睛】本题主要考查平行四边形、三角形高的画法。
33．6个
【分析】要求装20千克油至少需要几个这样的油桶，根据题意，也就是求20里面有多少个3.6，根据除法的意义用除法解答即可。注意结果用“进一法”取值。
【详解】20÷3.6≈6（个）
答：装20千克油至少需要6个这样的油桶。
34．186块
【详解】46.35÷0.25≈186（块）
35．8.4小时
【分析】根据速度×时间＝路程，求出西安到兰州的路程，再根据路程÷速度＝时间，求出返回时用的时间。
答：返回时用了8.4小时。
36．运进苹果158千克；香蕉92千克
【分析】设香蕉的质量是千克，苹果的质量是香蕉的1.5倍多20千克，则苹果的质量是千克；
用苹果的质量与香蕉的质量作和即可求出水果的总重量250千克，列出方程并解方程即可求出香蕉的质量；再用香蕉的质量乘1.5，再加上20千克，可求出苹果的质量。
【详解】设香蕉的质量是千克，则苹果的质量是千克
答：香蕉的质量是92千克，则苹果的质量是158千克。
37．750棵
【分析】平行四边形的面积公式为：面积＝底×高，菜地的底是25米，高是12米，代入公式可得菜地的面积为25×12＝300（平方米）。平均每平方米种2.5棵茄苗，总种植量＝菜地面积×每平方米种植数量。将菜地面积300平方米和每平方米2.5棵代入，用300乘2.5计算即可。
【详解】25×12×2.5＝750（棵）
答：一共可以种750棵茄苗。
38．552平方米
【分析】梯形的面积＝（上底＋下底）×高÷2，其中高是16米，上底与下底的和＝篱笆总长－高，据此解答。
【详解】（85－16）×16÷2
＝69×16÷2
＝1104÷2
＝552（平方米）
答：梯形的面积是552平方米。
【点睛】此题主要考查梯形的面积计算，先求出上下底之和是解题关键。