一、填空题（每空2分，共20分）
1. 3.6公顷 = ______平方米
2. 若甲数是乙数的2552，乙数比甲数多______%
3. 一个圆柱底面半径4cm，高10cm，体积是______cm³
4. 把7887 : 0.25化成最简整数比是______
5. 若x+13x=24x+31x=24，则x=______
二、选择题（每题3分，共15分）
6. 下列图形对称轴最多的是（ ）
A. 等边三角形 B. 正方形 C. 圆形
7. 某商品先提价10%，再降价10%，现价与原价比（ ）
A. 升高 B. 降低 C. 不变
8. 小明从家到学校，速度提高20%，时间减少（ ）
A. 16.7% B. 20% C. 25%
9. 能与1441 : 1661组成比例的是（ ）
A. 3:2 B. 2:3 C. 1221 : 1331
10. 右图长方体展开图缺少的面是______
A. 上面 B. 下面 C. 前面 D. 后面
三、计算题（共28分）
11. 简算（8分）
(1) 3.2×58+6.8÷1.63.2×85 +6.8÷1.6
(2) 201×78−78201×78−78
12. 解方程（8分）
(1) 0.4(x−1.5)=1.60.4(x−1.5)=1.6
(2) 2x+13=5−x232x+1 =5−2x
13. 图形计算（12分）
(1) 求阴影部分面积
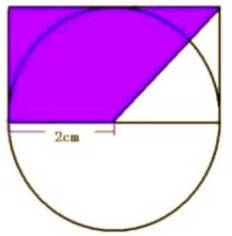
(2) 圆锥体积计算（底面直径8cm，高9cm）
四、应用题（共37分）
14. (8分) 甲乙两车从相距480km的两地相向而行，甲车速度60km/h，乙车速度比甲快25%，几小时后相遇？
15. (10分) 服装店售出两件衣服，A件盈利20%，B件亏损20%，总售价均为240元，整体是盈利还是亏损？具体数额多少？
16. (12分) 某校六年级学生参加兴趣小组统计：
编程组：占总人数15%
书法组：36人
美术组与体育组人数比4:5，且体育组比美术组多12人
求总人数及编程组人数
17. (7分) 观察数列：2，5，10，17，26...
(1) 写出第n项表达式
(2) 第10项是多少？
一、填空题
1. 36000
解析：1公顷=10000平方米，3.6×10000=36000
2. 150%
解析：设乙数5份，甲数2份，差3份，3/2×100%=150%
3. 502.4
公式：V=πr²h=3.14×4²×10=502.4
4. 7:2
步骤：7887:1441=7887×4=7:2
5. 18
解方程：43x=2434x=24 → x=18
二、选择题
6. C（圆形有无数条对称轴）
7. B（现价是原价的99%）
8. A（时间与速度成反比，1-1/1.2≈16.7%）
9. A（1441:1661=3:2）
10. A
三、计算题
11.
(1) 5+4.25=9.25
技巧：拆分计算 3.2×0.625=2；6.8÷1.6=4.25
(2) 78×(201-1)=15600
12.
(1) x=5.5
步骤：x-1.5=4 → x=5.5
(2) x=4
通分：两边×6得4x+2=30-3x → 7x=28
13.
(1) S阴影=S梯形，梯形的上底是圆的直径，下底、高是圆的半径，所以S阴影=1/2(2+4)×2=6(平方厘米)
(2) (2) V=1/3πr²h=150.72cm³
四、应用题
14. 4小时
解析：乙车速度60×1.25=75km/h，相遇时间480÷(60+75)=4h
15. 亏损20元
成本计算：
A件成本240÷1.2=200元
B件成本240÷0.8=300元
总成本500元＞总售价480元
16. 总人数180人，编程组27人
步骤：
设美术组4x，体育组5x → 5x-4x=12 → x=12
美术48人，体育60人 → 书法+美术+体育=144人（占85%）
总人数144÷0.85≈180人（验证比例）
17. (1) n²+1 (2) 101
规律：1²+1=2，2²+1=5，3²+1=10...
本试卷重点训练分数应用、比例问题、几何运算等核心能力，建议学生针对错题进行专项突破。
1. 3.6公顷 = ______平方米
2. 若甲数是乙数的2552，乙数比甲数多______%
3. 一个圆柱底面半径4cm，高10cm，体积是______cm³
4. 把7887 : 0.25化成最简整数比是______
5. 若x+13x=24x+31x=24，则x=______
二、选择题（每题3分，共15分）
6. 下列图形对称轴最多的是（ ）
A. 等边三角形 B. 正方形 C. 圆形
7. 某商品先提价10%，再降价10%，现价与原价比（ ）
A. 升高 B. 降低 C. 不变
8. 小明从家到学校，速度提高20%，时间减少（ ）
A. 16.7% B. 20% C. 25%
9. 能与1441 : 1661组成比例的是（ ）
A. 3:2 B. 2:3 C. 1221 : 1331
10. 右图长方体展开图缺少的面是______
A. 上面 B. 下面 C. 前面 D. 后面
三、计算题（共28分）
11. 简算（8分）
(1) 3.2×58+6.8÷1.63.2×85 +6.8÷1.6
(2) 201×78−78201×78−78
12. 解方程（8分）
(1) 0.4(x−1.5)=1.60.4(x−1.5)=1.6
(2) 2x+13=5−x232x+1 =5−2x
13. 图形计算（12分）
(1) 求阴影部分面积
(2) 圆锥体积计算（底面直径8cm，高9cm）
四、应用题（共37分）
14. (8分) 甲乙两车从相距480km的两地相向而行，甲车速度60km/h，乙车速度比甲快25%，几小时后相遇？
15. (10分) 服装店售出两件衣服，A件盈利20%，B件亏损20%，总售价均为240元，整体是盈利还是亏损？具体数额多少？
16. (12分) 某校六年级学生参加兴趣小组统计：
编程组：占总人数15%
书法组：36人
美术组与体育组人数比4:5，且体育组比美术组多12人
求总人数及编程组人数
17. (7分) 观察数列：2，5，10，17，26...
(1) 写出第n项表达式
(2) 第10项是多少？
答案详解
一、填空题
1. 36000
解析：1公顷=10000平方米，3.6×10000=36000
2. 150%
解析：设乙数5份，甲数2份，差3份，3/2×100%=150%
3. 502.4
公式：V=πr²h=3.14×4²×10=502.4
4. 7:2
步骤：7887:1441=7887×4=7:2
5. 18
解方程：43x=2434x=24 → x=18
二、选择题
6. C（圆形有无数条对称轴）
7. B（现价是原价的99%）
8. A（时间与速度成反比，1-1/1.2≈16.7%）
9. A（1441:1661=3:2）
10. A
三、计算题
11.
(1) 5+4.25=9.25
技巧：拆分计算 3.2×0.625=2；6.8÷1.6=4.25
(2) 78×(201-1)=15600
12.
(1) x=5.5
步骤：x-1.5=4 → x=5.5
(2) x=4
通分：两边×6得4x+2=30-3x → 7x=28
13.
(1) S阴影=S梯形，梯形的上底是圆的直径，下底、高是圆的半径，所以S阴影=1/2(2+4)×2=6(平方厘米)
(2) (2) V=1/3πr²h=150.72cm³
四、应用题
14. 4小时
解析：乙车速度60×1.25=75km/h，相遇时间480÷(60+75)=4h
15. 亏损20元
成本计算：
A件成本240÷1.2=200元
B件成本240÷0.8=300元
总成本500元＞总售价480元
16. 总人数180人，编程组27人
步骤：
设美术组4x，体育组5x → 5x-4x=12 → x=12
美术48人，体育60人 → 书法+美术+体育=144人（占85%）
总人数144÷0.85≈180人（验证比例）
17. (1) n²+1 (2) 101
规律：1²+1=2，2²+1=5，3²+1=10...
本试卷重点训练分数应用、比例问题、几何运算等核心能力，建议学生针对错题进行专项突破。