满分:100分 考试时间:80分钟 测试范围:第一、二、三、四单元
一、填空题(每小空1分,共24分)
1.下面的式子中哪些是方程。(填序号)
①4x-38;②32-2a=18;③a÷b=0.8;④1.4×1.2=1.68;⑤m-3.5<7.8 等式有( ),方程有( )。
2.若a、b都是大于0的自然数,a=7b,则a和b的最大公因数是( ),a和b的最小公倍数是( );b是非0自然数,若a=b+1,则a、b的最大公因数是( ),最小公倍数是( )。
3.暑假期间,王老师每6天返校一次,刘老师每4天返校一次。7月25日两人在学校相遇,至少再过( )天两人相遇,再次相遇时是( )月( )日。
4.有三个连续的奇数,如果中间一个数是a,其余两个分别是( )和( ),这三个连续奇数的和是( )。
5.7/8 的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
6.有18支铅笔,平均分给6个同学,每支铅笔是铅笔总数的 ( )/( ),每人分得的铅笔是铅笔总数的 ( )/( )。
7.有一个三位数37□,要使它既是2的倍数又是5的倍数,□里填( );要使它既是3的倍数,又是5的倍数,□里填( )。
8.一个花圃里有黄花a朵,红花比黄花的2倍多4朵,红花有( )朵,当时,两种花一共有( )朵。
9.把一张长48厘米、宽24厘米的长方形硬纸板,剪成边长为整厘米数的小正方形且没有剩余,至少可以剪成( )个小正方形。
10.华氏温度(°F)和摄氏温度(°C)的换算公式:华氏温度=摄氏温度×1.8+32,今天的气温是80.6°F,相当于( )°C;昨天的气温是30°C,相当于( )°F。
二、选择题(5分)
11.如果两个数的积是偶数,那么这两个数( )。
A.都是奇数 B.都是偶数 C.至少有一个是偶数
12.“一盒牛奶有 9/10 升”,9/10 升的意思是把( )看作单位“1”,平均分成10份,表示这样的9份。
A.1升牛奶 B.9升牛奶 C.10升牛奶 D.一盒牛奶
13.甲数比乙数的3倍多5,比丙数的5倍少3,乙数是47,甲数是( )。
A.136 B.145 C.10 D.146
14.用折线统计图反映( )比较合适。
A.某校各年级在校人数
B.南京某一天的气温变化情况
C.水果店4月份各类水果的销售量
15.如果用□表示一个质数,○表示一个合数,那么下面( )的结果一定是合数。
A.□+○ B.□-○ C.□×○
三、判断题(5分)
16.的和是偶数。( )
17.3千克的 1/4 比1千克的 3/4 重。( )
18.“一节课的时间是 2/3 小时”,是把一节课的时间看作单位“1”。( )
19.等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。( )。
20.15的因数有4个,15的倍数有无数个。( )
四、计算题
21.直接写出得数。 (8分)
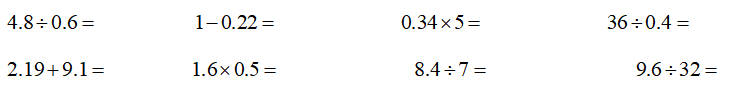
22.解方程。 (12分)
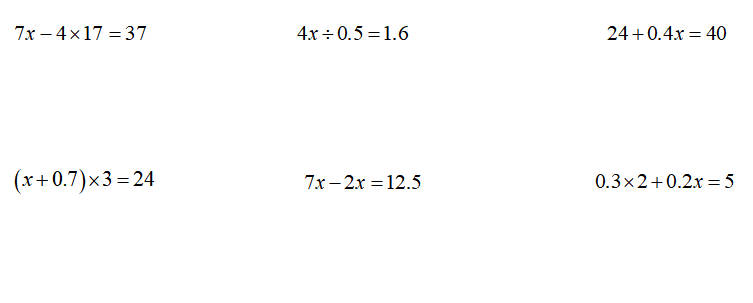
23.求下列各组数的最大公因数或最小公倍数。 (6分

24.某电器城2023年下半年空调和冰箱销售数量如下表。(8分)
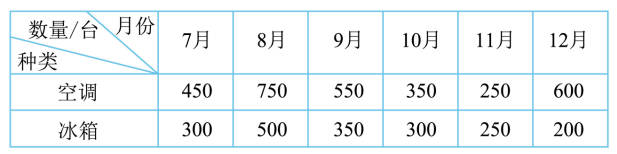
(1)根据上表中的数据制成折线统计图。
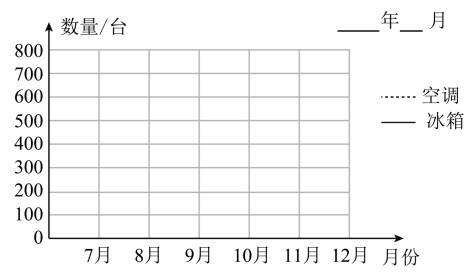
(2)平均每月销售空调大约( )台。(得数保留整数)
(3)如果每台冰箱获利100元,那么这个电器城2023年第三季度冰箱销售共获利( )
五、解答题(42分)
24.甲、乙两地相距546千米,客车和货车同时从两地相对开出,经过4.2小时相遇。客车平均每小时行70千米,货车平均每小时行多少千米?(列方程解答)
25.五(3班)有男生32人,女生28人。
(1)男生占全班人数的几分之几?
(2)女生占男生人数的几分之几?
26.一个比赛用足球的价格比一个训练用足球的价格贵76元。已知比赛用足球的价格是训练用足球价格的3倍,求这两种足球的价格?(用方程解)
27.一个长方形的池塘,长60米,宽42米,如果在它的四周及四角栽柳树,每相邻两棵树之间的距离要相等,那么最少要栽多少棵?如果每两棵柳树之间栽2棵桃树,那么桃树一共栽了多少棵?
28.把30厘米和48厘米的两根彩带剪成每段一样长的短彩带且没有剩余,每段短彩带最长是多少厘米?一共可以剪成多少段?
29.水果店运来苹果和梨共240筐,苹果的筐数是梨的5倍,苹果和梨各多少筐?(先画出线段图,再列方程解答)
参考答案

1. ②③④ ②③
【分析】含有等号的式子就是等式;含有字母的等式叫做方程,则只要满足是等式且含有未知数的式子就是方程,据此分析解答。
【详解】①4x-38,没有等号,不是等式也不是方程;
②32-2a=18,有等号且含有未知数,是等式也是方程;
③a÷b=0.8,有等号且含有未知数,是等式也是方程;
④1.4×1.2=1.68,有等号但是没有未知数,是等式不是方程;
⑤m-3.5<7.8,没有等号,不是等式也不是方程。
等式有(②③④),方程有(②③)。
2. b a 1 ab
【分析】当两个数是倍数关系时,较小的数是它们的最大公因数,较大的数是它们的最小公倍数;两个连续自然数互质,互质的两个数的最大公因数是1,最小公倍数是它们的乘积,由此得解。
【详解】若a、b都是大于0的自然数,a=7b,则a和b的最大公因数是(b),a和b的最小公倍数是(a);b是非0自然数,若a=b+1,则a、b的最大公因数是(1),最小公倍数是(ab)。
3. 12 8 6
【分析】至少还需要几天两人相遇,这个天数是6和4的最小公倍数。据此,先求出最小公倍数,再推算再次相遇是几月几日。
【详解】6=2×3
4=2×2
6和4的最小公倍数是:2×2×3=12
所以至少再过12天两人相遇。
7月还有:31-25=6(天)
8月还要:12-6=6(天)
7月25日再过12天是8月6日,所以8月6日他们又再次相遇。
4. a-2 a+2 3a
【分析】根据相邻的两个奇数之间相差2,可知如果中间一个数是a,其余两个分别是a-2和a+2;进而用加法计算即可求得这三个连续奇数的和。
【详解】有三个连续的奇数,如果中间一个数是a,其余两个分别是a-2和a+2;
(a-2)+a+(a+2)=a-2+a+a+2=3a;
答:这三个连续奇数的和是3a。
故答案为:a-2;a+2;3a.;
【点睛】任意两个相邻的奇数差是2,任意两个相邻偶数的差也是2。
5. 7 9
【分析】把单位“1”平均分成若干份取其中的一份的数,叫做分数单位。分子是几就有几个这样的分数单位。质数指的是只有1和它本身两个因数的数,最小的质数是2,据此可解答。
【详解】的分数单位是( ),它有( 7 )个这样的分数单位,再添上( 9 )个这样的分数单位就是最小的质数。
【点睛】本题考查分数单位及质数,明确它们的定义是解题的关键。
6.;
【分析】有18支铅笔,平均分给6个同学,求每支铅笔是铅笔总数的几分之几,用1除以18;
求每人分得的铅笔是铅笔总数的几分之几,把这些铅笔的支数看作单位“1”,用1除以6。
【详解】1÷18=
1÷6=
每支铅笔是铅笔总数的,每人分得的铅笔是铅笔总数的。
【点睛】求一个数是另一个数的几分之几,用这个数除以另一个数。
7. 0 5
【分析】根据2、3、5的倍数特征,个位上是0、2、4、6、8的数都是2的倍数;一个数各位上的数字之和是3的倍数,这个数就是3的倍数;个位上是0或5的数都是5的倍数;同时是2和5倍数的数,个位上必须是0;同时是3和5的倍数的数,个位上是0或5且各位上的数字之和是3的倍数,据此解答。
【详解】37□要使它既是2的倍数又是5的倍数,□内填0;
37□既是3的倍数,又是5的倍数,□内填0或5;
如果填0:3+7+0=10,10不能被3整除,370不是3的倍数,是5的倍数;□内不能填0;
如果填5:3+7+5=15,15能被3整除,375是3的倍数,也是5的倍数,□内填5。
有一个三位数37,要使它既是2的倍数又是5的倍数,里填0,要使它既是3的倍数,又是5的倍数,里填5。
【点睛】熟练掌握2,3,5的倍数特征是解答本题的关键。
8. 2a+4 28
【分析】由题意得出等量关系式:红花数量=黄花的数量×2+4,即2a+4;再用红花朵数加上黄花朵数即可求出两种花一共有多少朵。
【详解】a×2+4=(2a+4)朵
当a=8时
2a+4+a
=2×8+4+8
=20+8
=28
红花有(2a+4)朵;当a=8时,两种花一共有28朵。
【点睛】解决本题的关键是找出正确的等量关系式,再代数解答。
9.2
【分析】要把一张长48厘米、宽24厘米的长方形硬纸板,剪成边长为整厘米数的小正方形且没有剩余,只要求出48和24的最大公因数,就是正方形的边长,用48和24分别除以正方形的边长,得到的数相乘,就是至少可以剪成的小正方形的个数。
【详解】48和24的最大公因数是24,
即剪成的小正方形的边长是24厘米,
至少可以剪成:
(48÷24)×(24÷24)
=2×1
=2(个)
【点睛】此题考查的是最大公因数的应用,理解大长方形的长和宽的最大公因数即是小正方形的边长是解答此题的关键。
10. 27 86
【分析】由华氏度与摄氏度的换算公式是:华氏温度=摄氏温度×1.8+32,则摄氏度=(华氏度-32)÷1.8,据此计算解答。.
【详解】(80.6-32)÷1.8
=48.6÷1.8
=27(℃)
30×1.8+32
=54+32
=86(°F)
华氏温度(°F)和摄氏温度(°C)的换算公式:华氏温度=摄氏温度×1.8+32,今天的气温是80.6F,相当于27℃;昨天的气温是30°C,相当于86°F。
11.C
【分析】两个数的积是偶数,也就是积包含2这个因数,所以这两个数至少有一个数也包含2这个因数,据此解答。
【详解】A.例如3×3=9,3×5=15,不满足积是偶数的条件;
B.不一定都是偶数,如1×2=2;
C.至少有一个是偶数,如1×4=4,2×4=8。
故答案为:C
【点睛】解答本题的关键是理解和掌握奇数和偶数的概念及运用。
12.A
【分析】把1升牛奶看作单位“1”,把它平均分成10份,每份是升,升表示有这样的9份。
【详解】“一盒牛奶有升”,的意思是把1升牛奶看作单位“1”,平均分成10份,表示这样的9份。
故答案为:A
【点睛】本题是考查分数的意义及单位“1”的确定。把1升牛奶看作单位“1”,把它平均分成10份,每份是1升的,即升,十分之几升就是表示几份。
13.D
【分析】已知乙数是47,甲数比乙数的3倍多5,用47乘3再加上5即可求出甲数。
【详解】47×3+5
=141+5
=146
故答案为:D
【点睛】求一个数的几倍是多少,用乘法计算。根据甲数与乙数的数量关系即可解答。
14.B
【分析】折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;据此进行解答即可。
【详解】A.反映某校各年级在校人数的情况,用条形统计图比较合适;
B.反映南京某一天的气温变化情况,用折线统计图比较合适;
C.反映水果店4月份各类水果的销售量,用条形统计图比较合适。
故答案为:B
【点睛】此题应根据条形、折线统计图的特点进行分析、解答。
15.C
【分析】根据质数的意义:在自然数中,只有1和它本身两个因数,这样的数叫做质数;合数的意义:在自然数中,除了1和它本身,还有别的因数,这样的数叫做合数;1既不是质数也不数合数;据此解答。
【详解】□表示一个质数,○表示一个合数;
A.质数加合数可能是质数,也可能是合数;
B.质数减合数也可能是质数,也可能是1;
C.质数乘合数等于合数。
故答案为:C
【点睛】根据质数和合数的意义进行解答,关键明确,1既不是质数,也不是合数。
16.√
【分析】偶数个奇数相加得偶数,奇数个奇数相加得奇数,据此解答。
【详解】是18个奇数相加,根据“偶数个奇数相加得偶数”可知,的和是偶数。原题说法正确。
故答案为:√
【点睛】本题考查和的奇偶性。理解并掌握奇数和偶数的运算性质是解题的关键。
17.×
【分析】根据题意,把3千克看作单位“1”,平均分成4份,每份是它的,每份是(3÷4×1=)千克;把1千克看作单位“1”,平均分成4份,每份是它的,其中3份是它的,是(1÷4×30)千克。
【详解】3÷4×1=(千克)
1÷4×3=(千克)
所以,3千克的和1千克的一样重。原题说法错误。
故答案为:×
【点睛】正确理解分数的意义,是解答此题的关键。
18.×
【分析】根据分数的意义,小时表示把1个小时看作单位“1”,平均分成3份,取其中的2份,也可以表示把2个小时看作单位“1”,平均分成3份,取其中的1份。
【详解】“一节课的时间是小时”,不是把一节课的时间看作单位“1”,因为分数带单位,则把1个小时看作单位“1”,或者把2个小时看作单位“1”。原题干说法错误。
故答案为:×
【点睛】本题主要考查了分数的意义,明确分数带单位和没有带单位的区别是解答本题的关键。
19.√
【分析】等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【详解】等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。说法正确。
故答案为:√。
20.√
【分析】根据求一个数因数、倍数的方法解答即可。
【详解】15的因数有:1、3、5、15,共4个;15的倍数有:15、30、45……。所以15的因数有4个,15的倍数有无数个。
故答案为:√
【点睛】一个数的倍数的个数是无限的,最小的是它本身,没有最大的倍数;一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
21.8;0.78;1.7;90;
11.29;0.8;1.2;0.3
【详解】略。
22.x=15;x=0.2;x=40
x=7.3;x=2.5;x=22
【分析】7x-4×17=37,先计算出4×17的积,再根据等式的性质1,方程两边同时加上4×17的积,再根据等式的性质2,方程两边同时除以7即可;
4x÷0.5=1.6,根据等式的性质2,方程两边同时乘0.5,再同时除以4即可;
24+0.4x=40,根据等式的性质1,方程两边同时减去24,再根据等式的性质2,方程两边同时除以0.4即可;
(x+0.7)×3=24,根据等式的性质2,方程两边同时除以3,再根据等式的性质1,方程两边同时减去0.7即可;
7x-2x=12.5,先化简方程左边含有x的算式,即求出7-2的差,再根据等式的性质2,方程两边同时除以7-2的差;
0.3×2+0.2x=5,先计算出0.3×2的积,再根据等式的性质1,方程两边同时减去0.3×2的积,再根据等式的性质2,方程两边同时除以0.2即可。
【详解】7x-4×17=37
解:7x-68+68=37+68
7x=105
7x÷7=105÷7
x=15
4x÷0.5=1.6
解:4x÷0.5×0.5=1.6×0.5
4x=0.8
4x÷4=0.8÷4
x=0.2
24+0.4x=40
解:24-24+0.4x=40-24
0.4x=16
0.4x=16÷0.4
x=40
(x+0.7)×3=24
解:(x+0.7)×3÷3=24÷3
x+0.7=8
x+0.7-0.7=8-0.7
x=7.3
7x-2x=12.5
解:5x=12.5
5x÷5=12.5÷5
x=2.5
0.3×2+0.2x=5
解:0.6+0.2x=5
0.6-0.6+0.2x=5-0.6
0.2x=4.4
0.2x÷0.2=4.4÷0.2
x=22
23.18;17;1;
60;39;63
【分析】求两数的最小公倍数,就看两个数之间的关系,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积;
两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数;
或者先把要求的两个数分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【详解】因为18和36是倍数关系,
所以(18,36)=18。
因为51=3×17,34=2×17,
所以(51,34)=17。
因为13和4是互质数,
所以(13,4)=1。
因为15=3×5,20=2×2×5,
所以[15,20]=2×2×3×5=60。
因为13和39是倍数关系,
所以[13,39]=39。
因为7和9是互质数,
所以[7,9]=9×7=63。
24.60千米
【分析】设货车平均每小时行x千米,客车每小时行70千米,4.2小时行70×4.2千米;货车每小时行x千米,4.2小时行4.2x千米;客车4.2小时行驶的路程+货车4.2小时行驶的路程=甲、乙两地的距离,列方程:70×4.2+4.2x=546,解方程,即可解答。
【详解】解:设货车平均每小时行x千米。
70×4.2+4.2x=546
294+4.2x=546
4.2x=549-294
4.2x=252
x=252÷4.2
x=60
答:货车平行每小时行60千米。
【点睛】本题考查方程的实际应用,根据速度、时间和路程三者的关系,设出未知数,找出相关的量,列方程,解方程。
25.(1);
(2)
【分析】(1)把全班的总人数看成单位“1”,先把男女生的人数相加,求出总人数,再用男生的人数除以总人数即可求解;
(2)把男生的人数看成单位“1”,用女生的人数除以男生的人数即可求解。
【详解】(1)32÷(32+28)
=32÷60
=
答:男生占全班人数的。
(2)28÷32=
答:女生占男生人数的。
【点睛】此题属于分数除法应用题中的一个基本类型:已知两个数,求一个数是另一个数的几分之几。
26.比赛用足球的价格为114元,训练用足球的价格为38元。
【分析】设训练用足球价格为x元,则比赛用足球的价格为x+76元或3x元,根据比赛用足球的价格不变,列方程解答即可得训练用足球价格,再求比赛用足球的价格即可。
【详解】解:设训练用足球价格为x元。
x+76=3x
2x=76
x=38
38+76=114(元)
答:比赛用足球的价格为114元,训练用足球的价格为38元。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可。
27.34棵;68棵
【分析】(1)要求最少要栽多少棵,即每相邻两棵树之间的距离最大,即相邻两棵树之间的距离是60和42的最大公因数,求出60和42的最大公因数,即相邻两棵树之间的距离,即可求出应栽树的棵数;
(2)因为此长方形的池塘四周及四角栽柳树,可以看成是一个封闭的图形,所栽的柳树的棵数和间距数相等,用间距乘2即可解答出所种的桃树的棵数。
【详解】60=2×2×3×5
42=2×3×7
60、42的最大公因数是2×3=6
(60+42)×2÷6
=102×2÷6
=204÷6
=34(棵)
34×2=68(棵)
答:最少要种14棵柳树,桃树一共栽了68棵。
【点睛】关键是理解题意,明白是从求公因数作为突破口,进而找出解决问题的方法。
28.6厘米;13段
【分析】每段彩带最长的长度应是30厘米和48厘米的最大公因数,先把30和48进行分解质因数,这两个数的公有质因数的连乘积是这两个数的最大公因数;然后分别求出两根彩带分成的段数,进而把两根彩带分成的段数相加即可。
【详解】30=2×3×5
48=2×2×2×2×3
所以30和48的最大公因数是2×3=6,即每段彩带最长的长度应是6厘米。
30÷6+48÷6
=5+8
=13(段)
答:每段短彩带最长是6厘米,一共可以剪成13段。
【点睛】此题考查了求两个数的最大公因数的方法:两个数的公有质因数连乘积是最大公因数;数字大的可以用短除法解答.
29.苹果:200筐;梨:40筐
【分析】设梨有x筐,则苹果有5x筐。根据“苹果和梨共240筐”画图、列方程求解即可。
【详解】画图如下:
解:设梨有x筐,则苹果有5x筐。
x+5x=240
6x=240
x=40
5x=5×40=200
答:苹果有200筐,梨有40筐。
【点睛】本题主要考查列方程解含有两个未知数的问题。
30.(1)见详解
(2)491
(3)11.5
【分析】(1)根据统计表提供的数据,绘制统计图;
(2)根据平均数=总数÷数据个数,用7月到12月份卖出空调的总台数÷6,即可解答;
(3)先计算出第三季度冰箱销售的数量,再乘100,即可解答。
【详解】(1)如图:
(2)(450+750+550+350+250+600)÷6
=(1200+550+350+250+600)÷6
=(1750+350+250+600)÷6
=(2100+250+600)÷6
=(2350+600)÷6
=2950÷6
≈491(台)
平均每月销售空调大约491台。
(3)(300+500+350)×100
=(800+350)×100
=1150×100
=115000(元)
115000元=11.5万元
如果每台冰箱获利100元,那么这个电器城2023年第三季度冰箱销售共获利11.5万元。
手机端下载本试卷指南:
第一步:关注公众号 “学习需要百宝箱” 或者 在下面扫码关注!
第二步:进入公众号后,在下方输入:250403,获取下载链接地址,并点击下载即可!
第一步:关注公众号 “学习需要百宝箱” 或者 在下面扫码关注!

第二步:进入公众号后,在下方输入:250403,获取下载链接地址,并点击下载即可!
